 |  |  | Mitigation de Desastres en las Instalaciones de la Salud - Volumen 4 : Aspectos de Ingenieria (Pan American Health Organization (PAHO) / Organización Panamericana de la Salud (OPS), 1993, 87 p.) |  |  | Capitulo 2. Análisis y diseño de edificaciones hospitalarias | |  | Introducción | | | Análisis estático | | | Análisis espacial | | | (introduction...) | | | Análisis espacial estático | | | Análisis dinámico | | | (introduction...) | | | Espectros de respuesta | | | Sistemas de varios grados de libertad | | | Método simplificado | | | Diseño sismo-resistente | | | (introduction...) | | | Espectro de diseño | | | Comportamiento no lineal | | | Derivas y estabilidad | | | Optimación de seguridad y economía | | | Distribución de la energía | | | Disposición de la ductilidad | | | Duración del sismo | | | Aislamiento y control de vibraciones |
|
Mitigation de Desastres en las Instalaciones de la Salud - Volumen 4 : Aspectos de Ingenieria (Pan American Health Organization (PAHO) / Organización Panamericana de la Salud (OPS), 1993, 87 p.)
Capitulo 2. Análisis y diseño de edificaciones hospitalarias
Introducción
El análisis estructural de construcciones hospitalarias no difiere
en sus aspectos teóricos del correspondiente a una estructura corriente de
edificios, puesto que son construidas con idénticos materiales y sometidas a
cargas semejantes. Las diferencias pueden hallarse, más bien, en los criterios y
requisitos de diseño específicos para hospitales, con respecto a los cuales no
hay consenso en la comunidad internacional, tal como se expondrá más adelante en
este capítulo.
En lo que sigue a continuación ofrecemos en forma resumida los
principios básicos de análisis estructural adecuados para
edificios.
Análisis estático
Las estructuras sometidas a cargas estáticas, tales como las
representadas por el peso propio de la estructura y las cargas de uso, suelen
modelarse como estructuras hiperestáticas linealmente elásticas, para las cuales
es válido el principio de superposición. Esto permite relacionar las fuerzas y
las deformaciones a través de la fórmula simple:
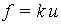
donde f es el
vector de fuerzas externas aplicadas a la estructura, u es el
vector de deformaciones de los puntos de aplicación de dichas fuerzas (grados de
libertad), y k es la matriz de rigidez definida como:
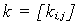
en la cual los elementos denotan la
fuerza en i cuando en j se da un desplazamiento
unitario.
El análisis usual para cargas de gravedad, así como para cargas
derivadas de empuje de tierras y agua y asentamientos diferenciales, recurre a
la ecuación antes expresada, bajo la suposición de linealidad en el
comportamiento esfuerzo-deformación de los materiales. Esta suposición es
adecuada en materiales como el acero y el aluminio a niveles moderados de
esfuerzo, por debajo del nivel de cedencia, ya que el módulo de elasticidad del
material es constante hasta dicho nivel. Para el concreto y la mampostería, la
suposición es menos adecuada, puesto que la pendiente de la curva
esfuerzo-deformación varía con el nivel de esfuerzo, pero el uso de la ecuación
es de todas maneras admisible.
Los términos elementales de rigidez utilizados hasta aquí son
usualmente modificados para tener en cuenta los siguientes hechos:
· La influencia de las deformaciones por
cortante, la cual es mayor a medida que aumenta la relación entre la altura de
la sección y su longitud.
· La gran rigidez de cada elemento en el sector del nudo, la
cual puede considerarse como infinita.
La matriz de rigidez de una barra prismática obtenida al tener en
cuenta estas dos modificaciones es la que usualmente se configura en los
programas de computador para el análisis de estructuras reticulares. J. Meek
(1) describe en detalle el análisis estructural por métodos matriciales,
así como los sistemas de cálculo
electrónico.
Análisis espacial
La naturaleza tridimensional de las estructuras de los edificios,
así como de las cargas de origen sísmico, ha creado la necesidad de realizar
análisis en tres dimensiones que reflejen de manera más adecuada que los
análisis planos el comportamiento de las estructuras.
La necesidad del análisis espacial se debe básicamente por el
fenómeno de la torsión. En efecto, la diferencia de disposición en planta de la
rigidez lateral hace que se presente torsión bajo la presencia de fuerzas de
inercia sísmicas o de viento, que por su naturaleza de fuerzas inerciales tienen
su resultante aplicada en el centro de masa de cada nivel, en términos
simplificados. La diferencia de posición entre el centro de masa y el punto de
concentración de la resultante de las fuerzas de reacción de los diferentes
elementos resistentes, hace que se genere un par instantáneo de rotación del
diafragma, el cual es mayor en la medida en que la distancia entre ambos puntos
aumente. El punto de aplicación de la resultante mencionada se conoce como
centro de rotación y su posición es, en general, variable, en dependencia de la
carga, la resistencia realmente ofrecida por los elementos en cada caso, etc.
Para la conversión del análisis espacial en una serie de análisis planos, puede
suponerse aproximadamente que dicho centro se encuentra localizado en el centro
de rigidez de los diferentes elementos que cruzan el diafragma (2). En el
caso de efectuarse un análisis espacial como el que se explica más adelante no
es necesaria dicha
suposición.
Análisis espacial estático
El siguiente desarrollo matemático supone que la losa de piso
ensambla las estructuras verticales resistentes (pórticos y muros) sin absorber
deformaciones, es decir, rígidamente. Esto supone que las fuerzas sísmicas son
enteramente absorbidas por las estructuras verticales y que la losa es
infinitamente rígida en su plano. Esta suposición, que se discute con mayor
detalle en el capítulo 3, está de acuerdo con lo observado en la mayoría de los
casos prácticos. La figura 1 ilustra este comportamiento rígido en una
estructura sin torsión así como un caso de comportamiento flexible de la losa en
su propio plano, el cual se considera indeseable. Puede verse claramente que
este caso requeriría de un análisis espacial en el que se considerara la
flexibilidad de la losa en su plano. Otros casos de este tipo de comportamiento
se describen en el capítulo 3.
FIGURA 1. COMPORTAMIENTOS RIGIDO Y FLEXIBLE DEL
DIAFRAGMA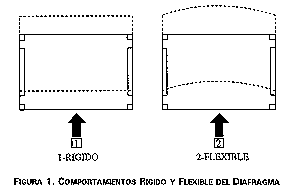
Supongamos que un sistema plano i, sometido a cargas
laterales, es analizado en sus dos coordenadas utilizando la matriz condensada,
por medio de la ecuación:
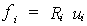
El vector de fuerzas puede ser
expresado en un sistema espacial de coordenadas, como:
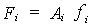
donde la matriz
Ai es la necesaria para transportar el
vector de fuerzas en el sistema local al centro de coordenadas del sistema
espacial. Por la ley del contragradiente, esta matriz es la misma que se
requiere para expresar la relación entre los desplazamientos en el sistema plano
y el espacial:
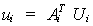
donde
Ui es el vector de desplazamientos de la
estructura plana vistos desde el sistema espacial. Reemplazando:
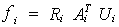
y premultiplicando por
Ai,
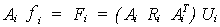
o, lo que es equivalente:
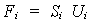
con:
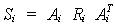
donde
Si es la matriz de rigidez de la
estructura plana expresada en términos del sistema de coordenadas espacial. De
manera semejante, al transportar todas las matrices de rigidez de los sistemas
planos al centro común se obtiene:
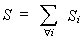
Las fuerzas sísmicas calculadas por medio del análisis dinámico o
del método simplificado, que se describen más adelante, se consideran aplicadas
en el centro de gravedad de cada piso, por su naturaleza de fuerzas inerciales.
El vector F es el vector de dichas fuerzas:
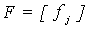
Los desplazamientos en el sistema
global producidos por estas fuerzas serán:
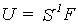
Los desplazamientos en cada uno de los
sistemas planos se obtendrán como:
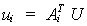
y los giros de los nudos se
calcularían de acuerdo con la ecuación:
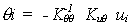
Con ambos resultados se calculan
fácilmente las fuerzas internas en los elementos del sistema
plano.
Análisis dinámico
Para las cargas de naturaleza sísmica es necesario recurrir a
análisis de tipo dinámico. Para el caso simple de vibraciones lineales no
amortiguadas y sin fuerza externa actuante, esto es, vibraciones libres, de un
sistema de un grado de libertad, se tiene:
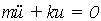
la cual tiene por solución:
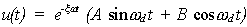
con:
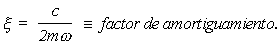
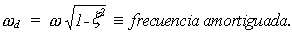
La vibración forzada, dada por:
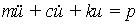
tiene por solución la integral de Duhamel:
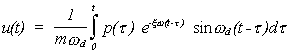
Por medio de derivación numérica se
obtienen las historias de velocidad y aceleración del sistema.
En el caso de movimientos del suelo, la fuerza dinámica tiene por
valor:
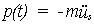
donde:
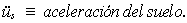
Por tanto,
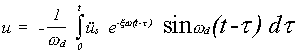
Un examen detallado de la dinámica de estructuras se encuentra en
Clough y Penzien
(3).
Espectros de respuesta
De la aplicación repetida de la integral de Duhamel para una misma
historia de aceleración del suelo y varios factores de amortiguamientos y
frecuencias, se obtiene múltiples historias de respuesta, cuyos valores máximos
suelen ser graficados contra sus respectivas frecuencias o períodos para tener
un reflejo de la acción del sismo sobre varios tipos de estructuras. Estos
espectros se definen como:
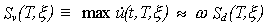
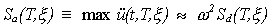
El mayor valor de las aceleraciones en una zona determinada de
períodos se debe a que las frecuencias naturales en ella se acercan a las
frecuencias dominantes de las ondas sísmicas en la base, condición necesaria
para que se presente una especie de resonancia del sistema con la excitación.
Las ondas sísmicas en la base de la estructura, a su vez, han sido filtradas por
el suelo sobreyacente a la roca basal y han adquirido por tanto las frecuencias
dominantes del mismo. Por esta razón debe considerarse con cuidado la relación
entre la frecuencia natural dominante de la estructura y la dominante del suelo.
La misma estructura, situada en dos suelos diferentes, puede responder con
mayores aceleraciones en un suelo que en otro, en dependencia de la relación de
su frecuencia natural con respecto a la del suelo (4).
La figura 2 muestra varios espectros de registros de sismos
obtenidos en diferentes tipos de suelos, normalizados según la aceleración
máxima del terreno. Se aprecia claramente que el efecto de la rigidez del suelo
es de doble naturaleza. Por una parte, determina la zona del espectro en la que
se dan los mayores valores de la respuesta, de manera tal que a mayor
flexibilidad del suelo, mayor período dominante en el espectro. Por otra parte,
la mayor flexibilidad del suelo impone una mayor amplificación de la aceleración
en la estructura.
FIGURA 2. ESPECTROS DE ACELERACION: COMPARACION DE EFECTOS DE
SITIO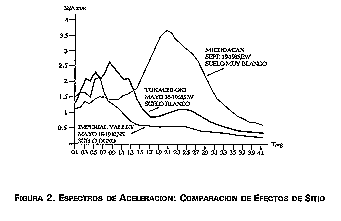
Sistemas de varios grados de libertad
La ecuación de vibración libre no amortiguada para sistemas de
varios grados de libertad toma la forma:
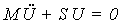
donde:
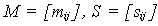
son las matrices de masa y rigidez,
respectivamente. Los términos de las matrices son las fuerzas en el grado de
libertad i debidas a una aceleración unitaria o a un
desplazamiento unitario, respectivamente, en el grado de libertad
j. El modelo adoptado normalmente es el mostrado en la figura 3.
Las masas tienen como grados de libertad dos traslaciones laterales ortogonales
y una rotación alrededor del eje central. Esto simula de manera adecuada los
desplazamientos de la estructura en el plano horizontal y la torsión de la misma
causada por excentricidades de la masa con respecto a la rigidez. La matriz de
rigidez, en consecuencia, se construye de acuerdo a estos grados de libertad,
tal como se ilustra más adelante. Sin embargo, puede ser suficientemente
satisfactorio usar un modelo plano para cada eje horizontal, y analizar los
efectos de torsión en un análisis espacial estático realizado con las fuerzas
resultantes de este análisis dinámico. En este caso, la matriz de rigidez es la
suma de las matrices de rigidez condensadas obtenidas para cada pórtico
resistente en el sentido del análisis:
FIGURA 3: MODELO DINAMICO ESPACIAL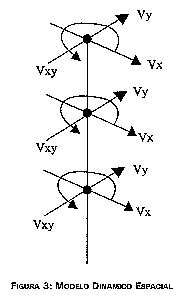
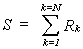
Si se supone la solución:
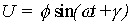
se llega a que:
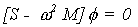
la cual tiene solución únicamente si:
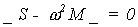
De la solución de este determinante se
obtienen las diferentes frecuencias de vibración, a cada una de las cuales
corresponde un modo de vibración. Físicamente, el significado del modo de
vibración es que, si la estructura se lleva a la posición de deformación
indicada por cada modo y se libera, vibrará de forma libre con la frecuencia
correspondiente y tomando en cada extremo de la vibración la forma del modo
respectivo.
Las fuerzas dinámicas actúan a través de las características
dinámicas de la estructura, esto es, de sus frecuencias y modos de vibración,
cada uno de los cuales representa un sistema de un grado de libertad. Por esta
razón, la respuesta total para vibraciones forzadas, según el principio de
superposición de sistemas lineales, será la suma de las respuestas individuales.
El valor total de la respuesta de desplazamiento está dado por:
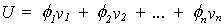
donde el primer factor de los términos
de la serie es el modo de vibración y el segundo representa la respuesta de
dicho modo a la excitación, y se conoce con el nombre de coordenada generalizada
del modo respectivo. De esta manera:
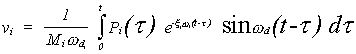
donde:
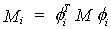
y:
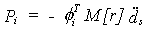
donde [r] es un vector
de influencia que representa los desplazamientos estáticos en los grados de
libertad de la estructura que resultan de un movimiento estático unitario en la
base. Para los modelos planos el vector [r] es un vector de unos.
De acuerdo a las ecuaciones de la dinámica de estructuras puede
demostrarse que la fuerza sísmica en el modo i y en el nivel
j es:
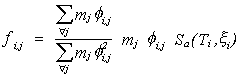
Las fuerzas máximas debidas a cada
modo no coinciden necesariamente en el tiempo, debido a la diferencia de
respuesta de cada modo, la cual a su vez se debe a la diferencia de frecuencias.
Por ello, su combinación para obtener la fuerza de diseño suele ser
probabilística. La manera usual de realizar esta combinación es por medio del
criterio de la raíz cuadrada de la suma de los cuadrados:
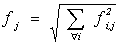
Sin embargo, en los últimos años ha
adquirido mayor aplicación la llamada combinación cuadrática completa, en la
cual:
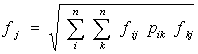
con:
Método simplificado
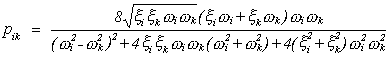
A partir de las fórmulas anteriores se puede derivar un método
simplificado de cálculo de fuerzas sísmicas. La fuerza debida al modo
i en el piso j puede expresarse también como:
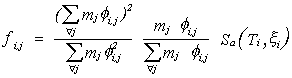
El primer término se conoce con el
nombre de masa modal efectiva del modo i. La tendencia usual en
edificios es que la masa efectiva del primer modo de traslación en cada sentido
constituya una gran parte de la masa total. Si se toma la masa efectiva del
primer modo como la masa total del edificio, y se asume que el primer modo tiene
forma lineal, expresada como la relación entre la altura del piso y la altura
total del edificio, de suerte que:
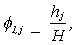
se obtiene:
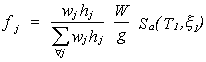
la cual es la fórmula básica de
cálculo de fuerzas en los métodos pseudo-dinámicos consagrados en varios códigos
de construcciones. El método logra evitar totalmente la realización de un
análisis dinámico al asumir el período fundamental de acuerdo a fórmulas
empíricas calculadas por experimentación de edificios con vibraciones
ambientales. Los partidarios del método lo defienden por su sencillez. Sin
embargo, al aumentar la complejidad de la construcción el análisis dinámico se
hace más necesario, debido a que el modo fundamental tiende a apartarse de la
forma asumida por el método simplificado y los modos superiores cobran mayor
importancia.
Diseño sismo-resistente
El diseño sismo-resistente de estructuras es de una complejidad
muy superior a la que caracteriza el diseño para cargas estáticas de gravedad,
debido a los múltiples factores que se deben tener en cuenta en él. Entre estos
se encuentran los siguientes:
a) La naturaleza azarosa de la excitación, en cuanto a
su momento de ocurrencia, localización, energía liberada, amplificación por el
suelo, variación con el tiempo, etc.
b) La incertidumbre sobre la respuesta de la estructura, debida a
la heterogeneidad de la calidad de los materiales, la interacción con los
elementos no estructurales, la variación de las cargas de servicio, las
variaciones presentadas en la construcción, etc.
c) Los mecanismos de falla y disipación de energía que impliquen
el menor riesgo para la vida humana y sus propiedades.
d) El costo en excedencia sobre la resistencia a cargas de
gravedad, implicado en evitar total o parcialmente el daño estructural y no
estructural.
e) El costo de reparación en caso de que se permita un nivel
determinado de daño.
f) El costo social implicado por la falla de edificios,
especialmente en el caso en que sean esenciales para la atención de un desastre,
como el caso de los hospitales.
De acuerdo con esto, el diseño sismo-resistente debe tratar de
atender de la mejor manera posible todos estos aspectos (5). Normalmente,
los códigos de diseño enmarcan algunos de estos problemas por medio de fórmulas
cuantitativas simples sobre seguridad global o local. El seguimiento estricto de
estas normas en el diseño habitual de estructuras, hace que el contenido de
fondo de tales simplificaciones sea frecuentemente desconocido u olvidado, lo
que da lugar a un trabajo de diseño rutinario e irreflexivo. Sin embargo, en el
diseño de cualquier edificio, y en especial en el de aquellos que deban
permanecer en el mejor estado posible después de un terremoto, debe tenerse
presente las implicaciones de cada decisión importante de acuerdo con los
principios y avances de la ingeniería sísmica, y bajo la óptica de la presencia
de la construcción en un medio social.
En el presente capítulo se revisan las implicaciones en el diseño
sísmico de hospitales de los aspectos mencionados
anteriormente.
Espectro de diseño
En el espectro de diseño recomendado por los códigos de
sismo-resistencia se encuentran implícitas decisiones sobre:
a) La probabilidad de excedencia del sismo de
diseño en un período de tiempo considerado como de vida útil media de los
edificios. Normalmente, se considera una probabilidad de excedencia del 10%
en un período de vida media útil de 50 años. En el caso de hospitales, sin
embargo, la vida útil supera ampliamente ese valor. La dinámica de la
construcción de centros hospitalarios es decididamente menor que la de
construcción de viviendas y otro tipo de construcciones. Esto es especialmente
crítico en los países en desarrollo, en los que la construcción de grandes
centros hospitalarios es escasa debido a que resulta altamente onerosa, por
diversas razones, y es, generalmente, deficitaria. Por estas razones la
perdurabilidad de dichos centros es muy alta en algunos países, y, en
consecuencia, debe pensarse con detenimiento la selección de estas variables.
b) Las frecuencias dominantes y respuestas máximas.
Normalmente, los espectros de sismos exhiben sectores estrechos de frecuencias
donde se encuentran las respuestas máximas. Sin embargo, para cubrir las
incertidumbres asociadas a la distancia de ocurrencia del evento y a su
contenido de frecuencias, los espectros de diseño presentan una amplia planicie
de respuestas máximas así como factores de amplificación de las respuestas en
terrenos blandos con respecto a las de terreno firme, de acuerdo a
comportamientos observados en varios sitios del mundo. No obstante, en el caso
de edificaciones especiales, puede ser conveniente la elaboración de un espectro
de diseño de acuerdo a las características geológicas y geotécnicas del sitio de
construcción.
Comportamiento no lineal
El criterio de diseño tradicional de edificios sometidos a sismos
fuertes ha sido el de permitir cierto ingreso de los materiales en el rango no
lineal con el fin de absorber energía bajo la especie de deformaciones
permanentes. La figura 4 ilustra este criterio para un sistema elasto-plástico.
La línea OA representa el diagrama esfuerzo máximo - deformación máxima de un
sistema perfectamente elástico en un sismo determinado, mientras que la línea
OCD representa un sistema elasto-plástico. Existen varias hipótesis sobre la
simplificación que debe ser asumida para evaluar de manera sencilla el
comportamiento del sistema elasto-plástico.
FIGURA 4. ABSORCION Y DISIPACION DE ENERGIA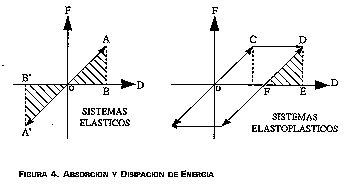
Hipótesis de igual deformación máxima. Si asumimos que un
sistema elasto-plástico, OAB (figura 4) tiene igual rigidez en su parte elástica
que el sistema elástico, esto equivale a que el período inicial del sistema
elasto-plástico es igual al período del sistema elástico. Si asumimos además que
los sistemas elástico y elasto-plástico tienen bajo el mismo sismo una igual
deformación máxima, OE=OB, entonces la siguiente relación es válida:
Es decir,
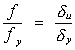
Si hacemos:
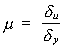
y lo definimos como factor de
ductilidad, la siguiente relación expresa las fuerzas de diseño del sistema
elasto-plástico:
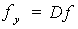
con:
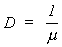
El factor D se denomina
usualmente factor de reducción de esfuerzos. De esta manera, la estructura debe
ser diseñada para unos esfuerzos menores que los dados por la respuesta del
sistema elástico, calculada de acuerdo a lo expresado en la primera parte de
este capítulo. Si con las fuerzas así obtenidas se realiza un análisis elástico,
se obtendrían unas deformaciones que, a su vez, deben ser multiplicadas por el
factor de ductilidad para estimar las deformaciones máximas de la estructura, lo
cual es de gran importancia para el estudio del comportamiento de elementos no
estructurales y la estabilidad de los diferentes pisos. Los elementos
estructurales deben entonces garantizar que se logre alcanzar dichas
deformaciones inelásticas. Para ello debe disponerse en dichos elementos de
ductilidad suficiente, por medio de los mecanismos que se detallará más
adelante.
Hipótesis de igual energía de deformación monotónica. En
este caso supondremos que la energía potencial almacenada en los dos sistemas,
de igual rigidez inicial y cargados monotónicamente, es equivalente. El área OAB
(figura 4) representa la energía elástica almacenada en el sistema elástico, la
cual se convierte en energía cinética que impulsa la estructura para movimientos
adicionales en la dirección opuesta, mientras que el área FED representa la
parte de la energía almacenada en el sistema elasto-plástico que es susceptible
de generar movimiento adicional. Puede verse que al ser menor la resistencia del
sistema, el sistema elasto-plástico deberá sufrir aceleraciones menores que el
sistema elástico. Por otra parte, el área FCDE representa la energía absorbida
por el sistema elasto-plástico por medio de deformaciones permanentes. Igualando
las dos energías totales, tenemos:
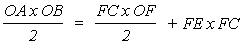
Es decir,
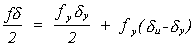
como:
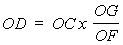
se llega finalmente a que:
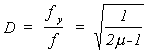
con:
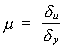
En consecuencia, la deformación máxima
del sistema elasto-plástico viene dada por:
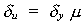
De esta manera se tienen diferentes
ecuaciones de la reducción de fuerzas que se debe aplicar en el diseño del
sistema elasto-plástico, así como de la deformación máxima del mismo.
Rosenblueth (6) recomienda utilizar la reducción de fuerzas según la
primera hipótesis para períodos largos y la segunda para períodos cortos. Para
el estimativo de desplazamientos inelásticos, es recomendable utilizar la
hipótesis más conservadora en cada caso.
Debe anotarse que estas son hipótesis de diseño establecidas en
muchos códigos de construcciones. Sin embargo, tienen el defecto de considerar
una reducción de fuerzas debido al comportamiento inelástico solamente en
relación con la deformación máxima alcanzada en cualquier instante del sismo, o
a la máxima energía disipada en un ciclo, sin atender a la duración de éste.
Esto hace que se dejen de lado factores tan importantes como los asociados a la
fatiga progresiva de los materiales, tales como la degradación de la rigidez, la
disminución de la resistencia, el aumento progresivo de las deformaciones, y por
ende, el colapso progresivo. Por esta razón, en los últimos años han adquirido
un gran énfasis los métodos que de una u otra manera involucran la duración
total del sismo en el diseño, generalmente a través de la energía total disipada
o del número de ciclos de
carga.
Derivas y estabilidad
En principio, los grandes desplazamientos laterales ponen en
peligro la seguridad de la construcción en su totalidad, debido al daño que
pueden representar para los elementos no estructurales en general. Sin embargo,
cuando son aún mayores traen consigo el riesgo de colapso parcial o total de la
edificación (figura 5).
FIGURA 5. DERIVAS Y ESTABILIDAD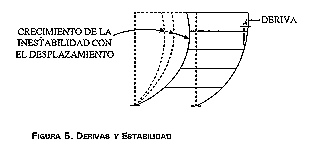
El daño en elementos no estructurales adosados a la estructura es
particularmente grave en el caso de hospitales, razón por la cual este tema será
tratado específicamente en el capítulo 3. Por lo pronto, es necesario tener
presente que dicho daño está asociado al valor del desplazamiento relativo
inelástico de un nivel con respecto al inmediatamente anterior, o deriva. Se ha
establecido que no son deseables valores de la deriva que superen el 1 o el 1,5
por mil de la altura libre entre los dos niveles. Sin embargo, este límite
depende estrechamente de la fragilidad y la resistencia de los materiales
componentes de los elementos no estructurales.
En lo que se refiere a la inestabilidad y efectos de segundo
orden, puede decirse suscintamente que éstos conducen al aumento de las derivas
de piso cuando el valor de dichos efectos es bajo, al incremento notorio de los
esfuerzos en los elementos estructurales en los niveles intermedios y al colapso
del piso (y, en consecuencia, del edificio en su conjunto posiblemente) en sus
niveles altos. Una manera sencilla de evaluar el grado de estabilidad de cada
piso de una construcción es por medio del índice de efectos globales de
inestabilidad:
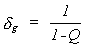
donde:
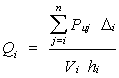
En esta ecuación,
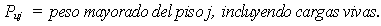
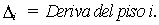
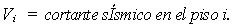
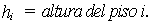
El valor de Q
relaciona, entonces, el incremento del momento de volcamiento del piso, de
acuerdo a un análisis somero de segundo orden, con el momento de volcamiento
directo o de primer orden. Puede considerarse que para valores de
Q menores de 0,3 el piso es estable, mientras que para valores
mayores de 0,5 es definitivamente inestable. La figura 6 muestra
cualitativamente el comportamiento del factor de amplificación por estabilidad
global con respecto al índice Q.
De acuerdo con lo anterior, para un análisis adecuado de los
problemas de derivas y estabilidad resulta de gran importancia el cálculo de
unos valores adecuados de desplazamiento inelástico. Según lo visto
anteriormente, y en vista de que los valores usuales del coeficiente de
reducción oscilan entre 0,17 y 0,5, el cálculo del desplazamiento máximo por
medio de la hipótesis de igual energía total con desplazamiento de cedencia
constante parece más adecuado para fines de diseño, debido a que arroja unos
valores más conservadores. Ser conservador en este aspecto es más conveniente en
el caso de hospitales que en los de otras construcciones, debido a las
implicaciones que los daños en elementos no estructurales y estructurales tienen
para los ocupantes y la comunidad en general.
FIGURA 6. FACTOR DE AMPLIFICACION DE ESFUERZO POR
INESTABILIDAD GLOBAL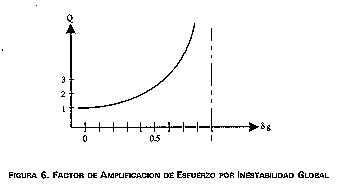
Optimación de seguridad y economía
Todo diseño de ingeniería debe buscar un adecuado balance entre
las condiciones de seguridad buscadas y las implicaciones económicas de la
dotación de tales condiciones. En el caso del diseño sísmico, el criterio para
la fijación de las condiciones de seguridad varía de acuerdo al tipo de
construcción a realizar. Así, para el caso de edificios de oficinas y uso
residencial, puede establecerse como criterio suficiente de seguridad la
protección de la vida humana, aceptando algunos daños estructurales y no
estructurales, mientras que en el caso de una central nuclear, la protección de
los equipos es de mayor importancia, más si se tiene en cuenta las consecuencias
que significaría su falla (7).
Particularmente, los hospitales deben ser diseñados de acuerdo a
condiciones de seguridad pertinentes no sólo a la seguridad de las personas que
lo ocupan en el momento de un terremoto, sino también a la necesidad de proveer
la atención médica de las víctimas resultantes como consecuencia de sismos
fuertes en una región amplia. Entre mayor sea la región de cobertura de un
centro hospitalario en caso de desastres, mayor debe ser su nivel de seguridad.
En general, para la determinación de la capacidad de un hospital debe
considerarse el incremento súbito que puede tener la demanda de sus servicios en
dicho caso. Esto lo ilustra la figura 7. La línea punteada denota la capacidad
del hospital y la línea gruesa la demanda, ambas en tiempos normales. Un diseño
para casos normales sería adecuado si, como se muestra en la figura la capacidad
instalada supera a la demanda normal. Sin embargo este puede no ser el caso de
muchos centros hospitalarios en países en desarrollo. El problema se agrava en
el caso de desastres que afecten a la infraestructura misma del hospital. En el
instante de un desastre sísmico la demanda aumenta abruptamente, mientras que la
capacidad de servicio puede decrecer como consecuencia de daños graves de la
estructura, suspensión de flujos eléctricos, de gas, de agua, daños de equipos e
instalaciones, caída de muros, cielos-rasos, etc., debido a decisiones u
omisiones en el diseño del hospital. El abismo entre la demanda incrementada y
la capacidad reducida puede ser mayor si la capacidad del hospital (considerada
en todos sus aspectos, tales como personal médico, camas, medicamentos, equipos,
etc.) es deficiente aún para tiempos normales, lo cual es también frecuente en
países en desarrollo.
FIGURA 7. RELACION DEMANDA CAPACIDAD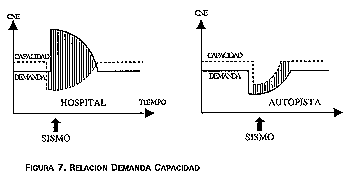
Como contraste, la figura muestra las curvas correspondientes a un
servicio público como la red vial, que puede ver disminuida su capacidad después
de un sismo fuerte, pero que, debido al impacto económico global sobre la
región, también registra disminución en su demanda. Por esta razón, en casos
como éste el abismo entre la demanda y la capacidad después de un sismo intenso
no es tan grave como en el caso de hospitales.
Finalmente, la curva de la demanda después del sismo es
descendente debido a la atención a las víctimas, pero bajo la condición de que
no se presenten varios sismos fuertes en un corto lapso, mientras que la
correspondiente a la capacidad es ascendente, en dependencia de la recuperación
del hospital. Ambas curvas están asociadas, pues la disminución de la demanda en
el tiempo depende de la recuperación de la capacidad. De nuevo, la situación
económica de la región afectada por el daño al centro hospitalario incide en
esta recuperación de la capacidad, la cual en consecuencia puede ser más o menos
rápida.
Todo lo anterior obliga a que las consideraciones sobre el nivel
de diseño de hospitales deban ser más o menos estrictas de acuerdo con su
responsabilidad social y nivel de desarrollo en cada caso. No es conveniente
extrapolar criterios de diseño sísmico de hospitales de unos países a otros ni
aun de unas regiones de un país a otras, sin consideración del impacto que en
cada una de ellas tenga determinado nivel de daño. De ahí que el llamado daño o
riesgo aceptable deba ser establecido en cada caso como una decisión de
planificación de la sociedad implicada.
Todo esto repercute en el diseño de ingeniería. Para fines de
decisión, el costo total de un hospital puede estimarse como:
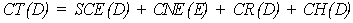
donde los términos indican el
sobrecosto estructural (SCE) por encima del requerido meramente para la
estabilidad ante cargas de gravedad, debido al elevamiento del nivel de diseño
con respecto a un diseño sísmico puramente elástico que no represente daño,
teóricamente; el costo de los elementos no estructurales (CNE) en general; el
costo de reparación (CR) y, finalmente, el costo humano (CH), entendido como una
conversión a valores económicos de las heridas y las pérdidas de vidas humanas.
Todos estos costos, con excepción del segundo, pueden considerarse dependientes
de una sola variable, D, es decir, el coeficiente de reducción de
fuerzas de diseño con respecto a un diseño elástico.
En el sobrecosto estructural debe tenerse en cuenta el incremento
de los esfuerzos de diseño de los elementos, de su rigidez y de su control de
construcción. Obviamente, este costo debe ser creciente con el factor
D. El costo de los elementos no estructurales es relativamente
insensible al factor D, y sólo aumenta levemente con el aumento de
los niveles de seguridad de equipos, instalaciones y muros, que podemos llamar
E. De todas maneras, es un costo que puede alcanzar valores muy
elevados, del orden del 60 al 80% del costo inicial del hospital. En el costo de
reparación, deben incluirse no sólo los costos de reparación física de la
edificación, sino también los de reposición de equipos e instalaciones
afectadas, así como el impacto en el tiempo de recuperación de estos daños. Al
contrario del anterior, se espera que este costo sea decreciente con el nivel de
seguridad dado a la construcción. Finalmente, en el costo humano se debe incluir
no sólo los afectados posibles que ocupan el hospital sino también, y con mayor
importancia, los heridos que se puede esperar sean enviados al centro
hospitalario en el caso de un desastre sísmico, de acuerdo con las cifras de la
planeación del mismo.
Los tres últimos costos son los que diferencian claramente el
diseño sísmico de un hospital del de un edificio común de uso residencial,
oficinas o comercio. Las figuras 8, 9 y 10 ilustran estas diferencias. Mientras
que las curvas de sobrecosto estructural pueden ser iguales o casi iguales para
los dos casos, las correspondientes a los elementos no estructurales es
notoriamente diferente, debido principalmente al valor de los equipos e
instalaciones hospitalarias, y registran un aumento con el nivel de seguridad
dado a los mismos, E. En cuanto al costo de reparación, la
pendiente de la curva debe ser en principio más pronunciada y de valores mayores
para los hospitales que para los edificios comunes, debido en mayor parte a las
implicaciones del daño de los equipos e instalaciones, que a la reparación de
daño estructural. Por último, el costo humano es radicalmente mayor en los
hospitales que en los edificios comunes por las razones anotadas.
FIGURA 8. COMPORTAMIENTO DE COSTOS I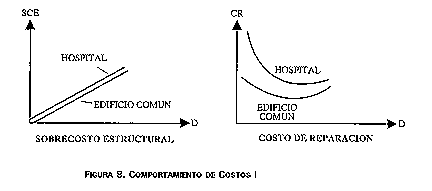
FIGURA 9. COMPORTAMIENTO DE COSTOS II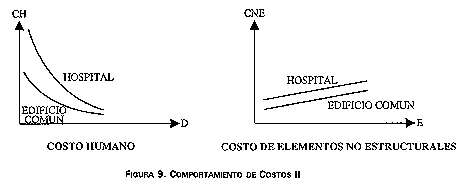
Al calcular el costo total para ambos casos, y compararlo con el
sobrecosto estructural, que gobierna de manera directa el diseño, puede verse en
la figura 10 que el punto de menor costo total se obtiene para edificios comunes
con una estrategia de diseño más tolerante de daño, mientras que para hospitales
dicho punto se obtiene con una estrategia menos liberal.
FIGURA 10. COSTO TOTAL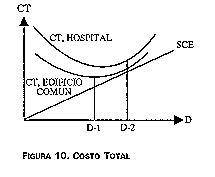
En principio, estudios de costos como el descrito anteriormente
deben emprenderse dentro del proceso de planificación de un hospital de
importancia en zonas sísmicas, con el fin de tomar las decisiones adecuadas con
respecto al nivel de seguridad estructural y que debe proporcionarse. En lo que
se refiere al nivel de seguridad no estructural, las pautas descritas en el
capítulo 3 son
suficientes.
Distribución de la energía
Las estimaciones sobre el comportamiento no lineal descritas
anteriormente tienen la desventaja de que inducen a extrapolar los resultados de
un sistema de un grado de libertad a sistemas de múltiples grados, como son los
edificios. Tal es el procedimiento de diseño recomendado en muchos códigos de
construcción, en los cuales se incorpora el uso de un factor de ductilidad
global para toda la estructura, cuando en realidad el daño o colapso de muchas
estructuras muestra un ingreso inusitado de ciertos sectores de la misma en el
campo inelástico, más allá de su capacidad de ductilidad, mientras que otros
permanecen en el campo elástico. Esto hace discutible el uso indiscriminado del
factor de ductilidad global para diversos tipos de estructuras, sin
consideración de sus condiciones de distribución de masa, resistencia o rigidez.
El método de energía total desarrollado por Akiyama (8)
tiene gran utilidad para determinar la distribución de la absorción de energía
en la estructura, en términos generales, con el fin de detectar las zonas
débiles de la misma. En principio, un diseño ideal sería aquel en el cual la
energía fuese absorbida en forma de deformaciones inelásticas en proporción y
forma similares por todos los pisos de la estructura, de manera tal que lo
correspondiente a cada cual sea lo menor posible. En este caso, el factor de
ductilidad alcanzado en el sismo sería semejante en todos los pisos. Sin
embargo, algunas circunstancias pueden alterar dicha uniformidad, y obligar a
que la energía se concentre en algunos pisos, los que así alcanzan factores de
ductilidad mucho mayores a los esperados, mientras que los restantes pueden
permanecer elásticos, de suerte que no se aprovecha en estos últimos su
capacidad de disipación de energía. Entre dichas circunstancias se encuentran:
· Distribución irregular de la masa, normalmente
con la presencia de pisos mucho más pesados que otros.
· Distribución irregular de la rigidez, de manera semejante
a lo dicho para la masa.
· Distribución de la resistencia de manera muy desviada de
un criterio considerado como óptimo para el desarrollo de una demanda de
ductilidad semejante en todos los pisos.
Igualmente, dentro de los pisos que absorben grandes proporciones
de energía puede haber algunos elementos que tomen más energía que otros,
haciendo así que hacia ellos se dirija el daño.
El método de energía utiliza en lugar de los espectros usuales, el
espectro de la energía suministrada a la estructura por el sismo:
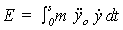
donde:
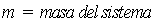
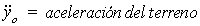
El
espectro de energía es definido de manera más conveniente en términos de una
velocidad equivalente:
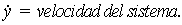
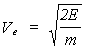
Como puede
verse, la energía inducida por el sismo depende no sólo de la aceleración del
terreno, sino además de la velocidad del sistema, el cual puede ser
elástico-amortiguado o no lineal. Una conclusión importante del estudio de los
espectros de energía es que los espectros inelásticos de diversos tipos de
no-linealidad (sistemas elasto-plásticos, sistemas deslizantes y combinaciones)
son cercanos en valores al espectro de energía de un sistema elástico con un
amortiguamiento del 10%. Esto simplifica de gran manera los cálculos.
La energía inducida en la estructura se descompone en las
siguientes partes:
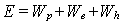
donde
Wp es la energía absorbida por
plastificación de la estructura, We es la
energía de respuesta elástica del sistema, y
Wh es la energía consumida por el
amortiguamiento.
De acuerdo con Akiyama (8), la distribución de la energía
absorbida por la estructura por medio de deformaciones inelásticas en el piso
i-ésimo, es una proporción de la energía total de plastificación,
mencionada más arriba, de valor:
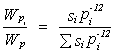
donde el factor p
califica la desviación del coeficiente sísmico del piso i-ésimo, de un
valor considerado como óptimo para el desarrollo simultáneo de igual ductilidad
en todos los pisos. La variable s reúne los datos sobre masa,
rigidez y capacidad de deformación inelástica de cada piso de la estructura.
La forma de la distribución de la energía arroja una gran claridad
sobre los pisos más débiles de la estructura, en los que puede concentrarse la
energía y por tanto, ser más probable el colapso. Para establecer la posibilidad
de éste resulta necesario calcular la demanda de ductilidad del piso bajo
análisis, la cual depende de la energía absorbida por el mismo.
La figura 11 muestra los resultados de cinco ejemplos de edificios
de 6 pisos evaluados por este método para aceleraciones del suelo del orden de
0,25 g. El caso 0 es el de un pórtico en el cual el coeficiente de diseño
sísmico de cada piso (definido como la relación entre el cortante de diseño y el
peso acumulado hasta ese piso) es el óptimo según el método (de acuerdo a
análisis de regresión). Es de anotar que los valores de dicho coeficiente óptimo
difieren fuertemente de los obtenidos por las fórmulas de diseño convencionales
de los métodos cuasi-estático y dinámico en los pisos superiores. La rigidez del
pórtico se ha disminuido gradualmente hacia arriba, de acuerdo a la menor
resistencia requerida, lo cual también se considera aconsejable. Puede verse que
los porcentajes de distribución de la energía son semejantes en todos los pisos.
FIGURA 11. CASOS DE CONCENTRACION DE ENERGIA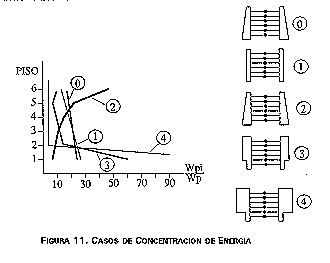
El caso 1 corresponde a un pórtico en el cual se ha mantenido la
rigidez y la masa constantes en toda la altura. En el caso 2, se ha colocado una
masa en el último piso cinco veces superior a la de los pisos restantes. El caso
3 presenta una rigidez en los pisos superiores tres veces superior a la del
primer piso, y en el caso 4 se ha aumentado esa diferencia a treinta veces.
Los resultados obtenidos indican claramente las desviaciones del
comportamiento óptimo. En el caso 0, la energía absorbida aumenta levemente
hacia el primer piso, lo cual es deseable debido al aumento de rigidez en el
mismo sentido. En el caso 1, este aumento se hace más brusco. En el caso 2, se
presenta un gran incremento de la energía absorbida en el último piso debido a
la alta concentración de masa en ese sitio. En los casos 3 y 4 se presentan
fuertes incrementos de la absorción de energía en el primer piso, causados por
la disminución de rigidez allí. Puede verse de esta manera que los resultados
del método concuerdan con las observaciones obtenidas en diferentes sismos sobre
el comportamiento de edificios
irregulares.
Disposición de la ductilidad
En vista de que los métodos de diseño no lineal simplificado
vistos anteriormente exigen la capacidad de la estructura de permitir grandes
deformaciones sin colapso, los elementos de la misma deben ser diseñados para
atender adecuadamente esta demanda de ductilidad.
A continuación examinaremos los mecanismos esenciales para la
obtención de altas capacidades de ductilidad en los sistemas estructurales
corrientes.
Estructuras de acero. A diferencia del concreto, el
acero es un material por naturaleza dúctil. Sin embargo, las grandes demandas de
ductilidad impuestas por los sismos hacen necesario el asegurar algunas medidas
especiales en los elementos estructurales. La más importante de ellas reside en
el diseño adecuado de las conexiones viga-columna. Las conexiones viga-columna
son el punto más vulnerable de las estructuras de acero sometidas a sismos. La
falla más común es la que ocurre por pandeo local en los patines y en el alma, y
tiende a suceder en la columna en su unión con la viga, debido a las fuerzas
trasmitidas por ésta. El diseño de la unión debe realizarse de tal suerte que la
rotación inelástica tenga lugar preferentemente en las vigas y no en la unión.
Para ello puede requerirse el uso de atiesadores horizontales y/o inclinados en
el alma de la columna con el fin de controlar la transferencia de esfuerzos de
un elemento al otro.
Estructuras de concreto reforzado. El concreto
reforzado se caracteriza por su escasa ductilidad, debido a su comportamiento
frágil ante grandes deformaciones. En el diseño de estructuras de concreto debe
detallarse con cuidado los mecanismos de ductilidad en los diferentes elementos,
de una manera más exigente que en el caso del acero. Los siguientes son los
criterios básicos para ello:
· Confinamiento. El confinamiento del
concreto garantiza la preservación del material ante la alternación de esfuerzos
dada en los terremotos y, en consecuencia, permite el desarrollo de
deformaciones inelásticas mayores que las posibles en una estructura en la que
el concreto se deteriore.
· Control de falla a cortante. La falla a cortante es
una falla que compromete seriamente la integridad de la sección de un elemento
cualquiera de concreto reforzado. Por esta razón los códigos de diseño
generalmente obligan a un diseño a cortante tal que garantice que la resistencia
a cortante sea superior a la resistencia a flexión. Esto se logra utilizando
como cortante de diseño un valor que sea como mínimo el correspondiente a la
plastificación por flexión en los nudos extremos.
· Control de la reducción de la ductilidad disponible
debido a la carga axial. La carga axial de compresión reduce drásticamente
la ductilidad de desplazamiento disponible en un elemento de concreto sometido a
ella. El fenómeno, que es más fuerte en columnas que en muros estructurales
generalmente, se debe a que a mayores cargas de compresión se reduce el trabajo
a tensión del acero, el cual puede darse con valores del esfuerzo de trabajo
menores del esfuerzo de fluencia, lo que implica un uso insuficiente del acero
para efectos de desarrollar grandes deformaciones inelásticas y disipar energía
por ese medio. Sin embargo, no siempre es posible diseñar las secciones de
columnas de manera que haya esfuerzos altos de tracción en el acero, por razones
arquitectónicas y económicas.
Park y Paulay (9) exponen ampliamente el comportamiento y
diseño del concreto reforzado sometido a vibraciones
sísmicas.
Duración del sismo
El efecto de la duración de un sismo en el comportamiento
estructural ha sido tradicionalmente ignorado en los códigos de diseño. Ello se
debe, en parte, a que el espectro de aceleraciones resulta insensible a la
duración del sismo, pues recoge solamente la información referente a la máxima
aceleración de respuesta ocurrida en algún momento del terremoto, e ignora lo
que sucede en adelante. Sin embargo, en sismos largos, pueden ocurrir complejos
fenómenos de degradación de la rigidez y la resistencia, debido al elevado
número de ciclos de carga que deben soportar los elementos estructurales. Debido
a ello, el diseño debería ser diferente para sismos cortos y largos,
independientemente de la aceleración de diseño.
De acuerdo a varios estudios realizados en diferentes países, la
duración de un sismo está en relación creciente con la magnitud del sismo y la
distancia epicentral. Al contrario, la aceleración del suelo decrece con dicha
distancia. De esta manera, pueden tenerse sismos de igual aceleración pico, lo
que produciría un igual espectro de aceleraciones de diseño, pero grandes
diferencias en la duración, lo que produciría efectos nocivos que no serían
detectados por dicho espectro. Esto conlleva a que, en el diseño de hospitales
se deba tener presente la información sismológica relativa a magnitudes y
distancias epicentrales de las fuentes probables de liberación de energía que
puedan afectarlos, de manera que si hay fuentes de magnitudes probables altas
situadas a grandes distancias epicentrales, pueden esperarse de ellas sismos
mucho más largos y, posiblemente, más destructivos que sismos cercanos. El sismo
de México de 1985 es no solamente una muestra de los efectos de amplificación
del suelo, sino también de los correspondientes a la alta duración, debido a la
alta magnitud (8.1) y lejanía del epicentro (350
km).
Aislamiento y control de vibraciones
Las técnicas de aislamiento en la base y control de vibración han
tenido un incremento notorio en su uso en construcciones localizadas en zonas
sísmicas en los últimos años, como alternativa a la disipación de energía por
medio de la tolerancia de daño por ingreso de los elementos estructurales en el
campo no lineal. Esto los convierte en sistemas que sin duda llegarán a ser de
gran importancia en la construcción de edificios en general, debido a las
crecientes exigencias de seguridad estructural y no estructural ante terremotos
fuertes, y de comodidad ante vibraciones ambientales. Pueden clasificarse en dos
grupos: sistemas de aislamiento y sistemas de control de vibración.
Estos sistemas de aislamiento son sistemas que
absorben la energía en la base de excitación por medio de grandes deformaciones,
amortiguamiento o combinación de ambos. Pueden clasificarse en los siguientes
subgrupos:
Sistemas de aislamiento en la base del edificio
Entre los dispositivos más corrientes utilizados para aislar los
edificios en la base se encuentran:
· Soportes de caucho y acero. Se trata de
soportes de alta rigidez y resistencia a carga vertical, lo que les permite
resistir las cargas derivadas del peso y uso de la construcción, mientras que su
alta flexibilidad ante movimientos horizontales permite que gran parte de la
energía del sismo se disipe en ellos. En algunos casos, el caucho tiene además
características de alto amortiguamiento, mientras que en otros el soporte tiene
un núcleo de plomo que realiza el papel de amortiguador, lo que hace innecesaria
la combinación con amortiguadores.
· Amortiguadores en la base. Pueden ser
amortiguadores de fricción, viscosos, o barras de acero flexible ancladas en
amortiguadores viscosos, que se colocan en la base del edificio con el fin de
reducir la energía sísmica en el edificio. En muchos casos son suficientes para
disipar la energía de vibraciones ambientales y sismos de poca intensidad, pero
para el caso de terremotos fuertes deben combinarse con los soportes de acero y
caucho. Su coeficiente de amortiguamiento puede alcanzar valores superiores a
30%.
Sistemas de aislamiento de entarimado de equipos
Los sistemas de aislamiento de entarimados consisten en
dispositivos cuyo fin es aislar las vibraciones de los entarimados donde se
encuentran equipos electrónicos y de precisión, que pueden ser averiados o
descalibrados por el movimiento dinámico. Su colocación se realiza entre la losa
y el entramado que soporta la tarima del equipo. Están compuestos por soportes
de caucho o de balines y/o amortiguadores viscosos para control de la vibración
horizontal y resortes de aire para la vibración vertical.
Los sistemas de control de vibración han sido ideados
principalmente para amortiguar las vibraciones eólicas, ambientales y sísmicas
en el interior mismo del edificio. Pueden clasificarse en los siguientes grupos:
· Sistemas de Control Pasivo
Los sistemas de control pasivo son adecuados para
vibraciones ambientales, pero en el caso de sismos no son generalmente útiles
más que para casos de moderada intensidad. Entre ellos se encuentran los
siguientes mecanismos:
· Amortiguadores estructurales pasivos.
Se trata de amortiguadores de diferentes materiales (acero flexible al corte,
caucho de silicona, caucho plástico, caucho bituminoso, etc.) que se colocan
generalmente debajo de los diafragmas de piso, con el fin de participar en la
absorción de la energía inducida de manera uniforme en toda la altura del
edificio.
· Amortiguadores de palanca. Consisten en
amortiguadores que convierten el movimiento horizontal de la estructura en un
movimiento vertical amplio de amortiguadores verticales dobles colocados en los
extremos de una palanca, cuya viscosidad permite la reducción de las
vibraciones.
· Péndulos resonantes pasivos. En este sistema, el
control de la vibración se efectúa por medio de la colocación de un péndulo de
gran masa, cercana al 1% de la masa total del edificio, en la azotea del mismo,
y diseñado con un período igual al de la estructura, con el fin de que entre en
resonancia. Con ello se obtiene la máxima eficiencia del péndulo, puesto que
éste, debido a su rigidez nula, induce una fuerza inercial contraria a las
fuerzas elásticas de la estructura, en su punto más alto. Así se obtiene una
fuerza que equilibra al menos en parte las fuerzas inerciales derivadas del peso
de la construcción. Entre los sistemas usados se encuentra el péndulo simple con
masas de acero o concreto, péndulos múltiples o tanques de agua con control de
vertimiento. En este último caso el tanque puede ser usado como tanque normal de
reserva de agua en el edificio.
· Sistemas de Control Activo
Los sistemas de control activo se diferencian de los anteriores en
el hecho de que adecuan las condiciones de trabajo a la excitación, de acuerdo a
las lecturas de sensores colocados en diversas partes del edificio, y cuyas
señales son leídas y analizadas por computador. Por norma disponen de fuentes
alternas de generación de energía eléctrica, para evitar las consecuencias de
cortes de suministro en el caso de sismos fuertes. Entre ellos son dignos de
mención los siguientes tipos:
· Péndulos activos. Se trata de péndulos
como los descritos anteriormente, que incorporan una fuerza activa contraria a
las fuerzas inerciales de la estructura en cada ciclo, fuerza que el sistema de
control automático calcula por medio del computador a partir de las señales
suministradas por los sensores.
· Controladores estructurales activos. Consisten en
diagonales de acero conectadas a un mecanismo que recibe las señales del
computador y los sensores. El mecanismo tiene como fin modificar la rigidez de
las diagonales de acuerdo a las señales con el fin de alejar a la estructura de
la zona de resonancia en cada
ciclo.
